Improved Scheduling of Robotic Telescopes
New Observing Modes for the Next Century
ASP Conference Series, Vol. 87, 1996
T. A. Boroson, J. K. Davies, and E. I. Robson, eds.
(*) Recom Technologies, MS 269-2, NASA Ames Research Center, Moffett Field, CA 94035>
(+) Center for Automated Space Science and Center of Excellence in Information Systems, Tennessee State University, 330 10th. Avenue North, Nashville, TN 37203
Abstract
The Automatic Telescope Instruction Set defines a simple but effective heuristic dispatch scheduler for determining the order in which observations are made. This scheduler has been found to perform well under some circumstances, but there are circumstances under which it performs rather poorly. This paper outlines a new schedule generation and execution framework that allows ATIS telescopes to operate using any desired scheduling technique. This paper also presents one particular alternative scheduling technique that generally outperforms the ATIS heuristic dispatcher. The performance of this new scheduler is compared to ATIS dispatch under a variety of circumstances.
Introduction
The Automatic Telescope Instruction Set (ATIS) is a language for specifying astronomical observations and the conditions under which those observations can be made (Boyd et al., 1993). ATIS allows an astronomer to package related observations as a group. Each group has a set of preconditions that determine when it can be executed. These preconditions include the Julian Date range over which group observations can be made, the hour angle limits that are suitable for the group, the maximum number of times the group should be executed within a night, a relative priority, and a statement as to whether or not group observations can be made when the moon is up.
The ATIS standard also defines a method for sequencing the execution of a set of groups. This technique, a form of heuristic dispatch, has been used with excellent results for several years. However, Henry (this volume), has recently demonstrated that there are circumstances under which the ATIS dispatch technique does not perform well. In this context, our paper has two contributions. First, we present an extension to the original ATIS model that allows for the use of alternative scheduling techniques. Second, we present one such technique. The alternative we present is based on a form of heuristic search called greedy search. This paper compares the performance of a scheduler based on greedy search to that of ATIS dispatch.
A New Approach
One problem with ATIS is that the dispatching scheduler is "built-in", with no way to remove or override it. We became involved with ATIS precisely to help with this problem. ATIS89, the original ATIS, first defined the heuristic dispatching technique (see Henry, this volume). We were involved in the International Astronomical Union committee that formalized ATIS93, and our goal was to make it possible to replace the ATIS dispatcher. We achieved this by means of a single new ATIS advice statement that allows for a schedule to be communicated to an ATIS-speaking telescope.
Each advice statement is essentially a numbered rule that says: if the current local sidereal time is greater than T1 but less than T2 then execute group G next, and then check advice statement N. (See Bresina et al., 1994, for more detail.) Each rule "points" to another rule, and these pointers define the expected sequence, or schedule, of group executions. In control theory (Dean & Wellman, 1991) or in decision theory (Russell & Wefald, 1991), a set of such rules is often called a policy. Formally, a policy is a function that maps from states of the world into actions that should be taken in those states. The ATIS93 advice statement provides a means of encoding a policy and communicating it to an ATIS-speaking telescope. A set of advice statements can be constructed using a wide variety of different algorithms. In general, if a scheduling algorithm generates advice statements for an ATIS-speaking telescope, we say that it is external (to the telescope).
Given a policy encoded by a set of ATIS93 advice statements, a set of ATIS groups must now be executed in a slightly different way. If there are no advice statements, then ATIS93 says that the telescope falls back to using its existing dispatch technique; thus, ATIS93 does not strictly require an external scheduler, but can use one if it is available. If there are advice statements generated by an external scheduler, then they must be followed. Following advice statements means ensuring that the current advice statement covers the current time, executing the group that it recommends, and following its pointer to the next advice statement in the sequence. If the current recommended advice statement does not apply, then the schedule is said to be broken. Under this circumstance, the telescope controller can ask the external scheduler for a new schedule (see Boyd et al., 1993 for the details). If the external scheduler takes too long to respond or never responds at all, then the telescope controller can also simply fall back on its built-in dispatching technique. With this design, it is possible to override the behavior of the default ATIS dispatcher, without the telescope being held hostage by an ill-behaved external scheduler (or an ill-behaved communication link to that scheduler). The telescope controller remains in control, and it can ask for advice from the external scheduler as it sees fit.
This approach to overriding the default behavior of an ATIS-speaking telescope is being implemented in the Associate Principal Astronomer, a system for managing remotely located, fully automatic telescopes (Drummond et al., 1995). There are many aspects of the APA that are not central to the task of observation scheduling, and these are not discussed here.
A Scheduler Based on Greedy Search
To apply a greedy search approach to the ATIS group scheduling problem, we must first define a space of possible states and a transition function that maps from state to state in that space. In our formulation of the ATIS group scheduling problem, each state contains the local sidereal time at the telescope and a counter for each group that indicates how many times that group has been scheduled (up to that time). A transition from one state to another in this search space models the execution of a single ATIS group. Each state in this space corresponds to a single partial schedule. More precisely, a given state corresponds to the schedule that contains each group labeling the trajectory that connects the unique initial state to the given state. During search, it is relatively easy to construct each successor state as required: the time for a new state is computed from the current state plus the expected duration of the group, and the execution counter of the given group is incremented by one.
Given this definition of a search space, a greedy search procedure operates as follows. In a given state, compute all enabled groups. An enabled group is one whose preconditions are met. These preconditions include all those enforced by the ATIS dispatcher, viz, Julian Date window, hour angle window, maximum execution count, and the moon status (up, down, or either). For each enabled group, apply that group, and create a successor state. Next, for each successor state, apply some given evaluation function that returns a score reflecting the degree to which that state satisfies some given set of preference requirements. Select the state that scores best, make it the current state, and repeat the entire enablement, application, and selection process. This algorithm terminates when there are no more enabled groups. For the search space that we have formulated, this happens at (simulated) dawn.
The performance of greedy search hinges critically on the definition of the heuristic evaluation function used to select among successor states. This evaluation function encodes preferences with respect to telescope performance. Our evaluation of a state is based on analysis of properties of the group giving rise to that state and the predicted time the group will start executing. Our implementation of greedy search allows the heuristic evaluation function to be parametrically expressed as F(S) = w1 * f1(S) + ... + wn * fn(S). The overall heuristic evaluation function F is applied to each successor state, S. That function is a weighted summation of different attribute functions, the fi. Each fi evaluates the state on some different property and it is possible to set the wi as "weights" in order to express relative importance of the attributes. We have identified a number of potentially useful attribute functions, but here we restrict our discussion to three: airmass, priority, and run count.
The airmass attribute of the evaluation function measures how the airmass of a schedule deviates from a desired pointing "track" as a function of time through the night. The basic idea for this track is that, typically, the telescope should start in the west, observing objects that are late in their season. In the first part of the night, the telescope should move toward the meridian, crossing the meridian at some point during the night. The telescope should then track to the eastern observing limit, making observations on objects that are early in their observing season. The telescope should arrive at the eastern observing limit at dawn.
Our implementation of this concept provides a simple graphical mechanism to define the desired telescope pointing track across the sky. Using this mechanism, it is possible to define the proportion of the night that should be spent on season extension in the west, the proportion of the night that should be spent on the meridian, and the proportion of the night that should be spent on season extension in the east. If each season extension proportion occupies half the night, then a diagonal line has been defined, running from west to east, that attempts to maximize season extension and accepts higher airmass observations. If the proportion of the night given over to season extension (in both the west and east) is small, then a pointing track has been defined that attempts to make observations at the lowest possible airmass, and thus, of the best possible data quality. Of course, this increase in data quality is accomplished at the expense of season extension.
The airmass score for a state is computed from the group giving rise to that state and the group's predicted start time. The score is the difference between the desired track and the predicted pointing angle of the telescope at the start of the group's execution. The weight of this attribute (in the overall evaluation function) makes it possible to express how important it is for the scheduler to attempt to achieve the specified pointing track across the sky.
The priority and run count attributes are much simpler. The priority score for a state is simply the priority of the group giving rise to that state. In ATIS, lower numbers indicate higher priority. The run count score for a state is the number of times the group (giving rise to that state) has been previously scheduled. Lower run count scores favor running each group once before running any group twice. Lower scores for all three attributes are preferred; hence, the successor state that minimizes the weighted sum of the attribute scores is chosen.
Performance Results
Why should greedy search outperform ATIS dispatch? There are two main reasons. First, this approach combines a set of disparate attributes in a weighted evaluation function, instead of making a choice based primarily on priority, using other attributes only to break ties. The weighted evaluation function more reasonably combines different factors that together determine the overall quality of a schedule. Second, the dispatcher has no notion of a desired airmass track. As Henry (this volume) has shown, when the dispatcher is overloaded the telescope never makes it as far as the meridian. When the dispatcher is underloaded the telescope thrashes back and forth across the sky. Giving the scheduler a reference pointing track should help to improve telescope performance.
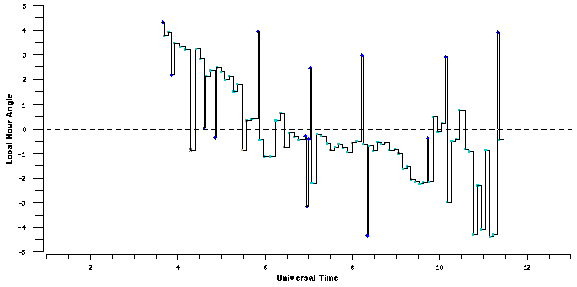
| |
| Figure 1: Hour-angle track of the Vanderbilt/TSU 0.4-m APT for the night JD 2449889, as scheduled by greedy search. Except for a few necessary excursions to the east and west limits to observe standard stars (marked by filled circles), the telescope moves smoothly from the west to the east hour-angle limits during the 7.5-hr night. | |
For comparison, see Figure 1, where the hour-angle track of the telescope is shown as a function of universal time. The Julian Date for this plot is one where the moon is not a factor, and the resulting observing load is handled extremely well by the ATIS dispatcher. See Henry (Figure 1, this volume) for an account of the dispatcher's performance on this same night. Henry, after significant experience with the dispatcher, judges its performance to be close to optimal for this night. Given this, the best we can hope for with greedy search is a tie. Figure 1 confirms that the performance of greedy search is quite comparable to the dispatcher's: the telescope starts in the west, observing objects before they set, works its way smoothly to the meridian, and then continues on to the eastern observing limit, arriving there at dawn. Deviations from this smooth track are standard star observations, which must be made at a variety of airmasses at different times throughout the night. Comparing the performance of greedy search with that of the dispatcher for this particular night, we conclude that the two techniques perform equally well.
Figure 2 shows performance in terms of hour-angle versus universal time for a night where the telescope is significantly underloaded due to the presence of the moon. Many of the groups in the load require the moon to be down, so when the moon is up, those groups are disabled. Henry (Figure 2, this volume) shows how the ATIS dispatcher tends to produce a "thrashing" behavior for such a night. Given the way that our greedy search algorithm uses a desired pointing track, we would expect it to avoid this thrashing behavior, despite the fact that the telescope is underloaded. Indeed, and as the figure shows, the performance of greedy search on this underloaded night is much the same as for the optimally loaded night. Except for a few necessary standard star observations that deviate from the desired pointing track, the telescope achieves a reasonable compromise between season extension and minimum airmass.
It is important to understand that both ATIS dispatch and the greedy search approach must repeat groups on an underloaded night; there are simply too few groups to fill the night, so some groups must be executed more than once. The real performance difference between the techniques arises from where they choose to make repeat observations. The dispatcher repeats observations at high airmass, while greedy search attempts to stick to the given pointing track. Thus, while both techniques eventually fill the night with observations, the quality of the data obtained by greedy search can be expected to be significantly better than that obtained by the dispatcher.
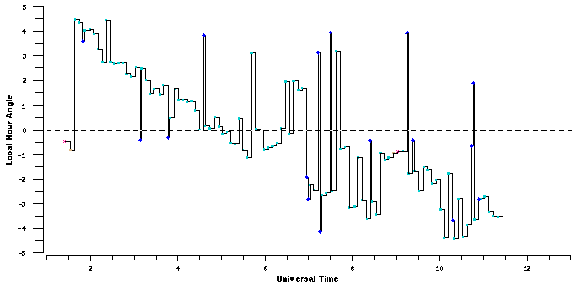
| |
| Figure 2: Scheduler hour-angle track of the Vanderbilt/TSU 0.4-m APT for the night JD 2449705. Except for standard star observations (marked with filled circles), the telescope moves smoothly from west to east observing program stars until it reaches the eastern hour-angle limit at dawn. In contrast, the ATIS dispatching technique tends to produce a thrashing behavior due to underloading (caused by the moon). As a result, the mean airmass of the observations is less than is achieved by the dispatcher. | |
We must more precisely quantify the relative performance of the ATIS dispatcher and the greedy search approach. We have developed a technique for comparing the performance of schedulers (Bresina et al., 1995) and have applied it to one instance of the ATIS group scheduling problem, but plan to apply and evaluate it more extensively. Our next step in this regard is to run a number of comparative scheduling experiments over a full lunar cycle and to more precisely measure the expected improvement in average airmass.
One advantage of ATIS dispatch is that it is robust: schedules never break during execution, since precise expectations about the future are never formed. Dispatch operates purely reactively, by choosing a group appropriate to the telescope's current state. In contrast, a schedule expressed as a set of advice statements (in ATIS93) is built on an expectation regarding how long each group takes to execute. If this expectation is wrong, then the schedule might break during execution. We have a technique for dealing with this and it has performed well in extensive simulation (Drummond, et al., 1994), but it has yet to be tested in practice.
Also, we have realized that it is rather hard to specify a load-independent pointing track. The desired pointing track is actually a function of the telescope load, calculated in terms of right ascension clumping of observing targets. Our next step is to form the desired hour angle track automatically, computing it from a loading analysis of the groups that are enabled on a particular night.
Acknowledgments
Thanks to Bob Morris for calibrating the greedy search algorithm's evaluation function weights, and thanks to Keith Swanson for helping get this project underway. The development of new scheduling techniques for automatic telescopes is supported through NASA grant NCC 2-883 to TSU. Automated astronomy at TSU has been supported most recently through NASA grants NAG 8-1014 and NCCW-0085 and NSF grant HRD-9550561.
References
Boyd, L., D. Epand, D., Bresina, J., Drummond, M., Swanson, K., Crawford,D. Genet, D., Genet, R., Henry, G., McCook, G., Neely, W., Schmidtke, P., Smith, D., and Trublood, M. 1993. IAPPP Comm. No. 52, p. 23.
Bresina, J., Drummond, M., Swanson, K., and Edgington, W. 1994. In Optical Astronomy from the Earth and Moon, ASP Conference Series, Vol. 55. D.M. Pyper and R.J. Angione (eds.).
Bresina, J., Drummond, M., and Swanson, K. 1995. Expected Solution Quality. IJCAI-95, Montreal, Canada. Morgan Kaufmann Publishers Inc., San Mateo CA.
Dean, T. and Wellman, M. 1991. Planning and Control. Morgan Kaufmann Publishers Inc., San Mateo CA.
Drummond, M., Bresina, J., and Swanson, K. 1994. Just In Case Scheduling. AAAI-94, Seattle, WA. AAAI Press.
Drummond, M., Bresina, J., Edgington, W., Swanson, K., Henry, G., and Drascher, E. 1995. In Robotic Telescopes: Current Capabilities, Present Developments, and Future Prospects for Automated Astronomy, ASP Conference Series No. 79. G. W. Henry and J. A. Eaton (eds.).
Russell, S. and Wefald, E. 1991. Do the right thing: Studies in Limited Rationality. MIT Press, Cambridge MA.